CBSE Class 10 Mathematics Chapter 9 Some Applications of Trigonometry Exercise 9.1

 

Q1.

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).

Ans.

Given :  Length of rope = Hypotenuse = AC = 20 m The angle made by the rope with the ground level = $\angle BCA = 30^{0}$ We have to find Height of pole = AB = let, h Using trigonometric ratios of $\sin\theta = \frac {\text {Opposite side to}\angle C}{Hypotenuse}=\frac {AB}{AC}$ Putting value $$\sin(30^\circ) = \frac{h}{20}$$ Solving for $h$: $$h = 20 \cdot \sin(30^\circ)$$ $$h = 20 \cdot \frac{1}{2}$$ $$h = 10 \, \text{m}$$

Q2.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

Ans.

Construction: By using given instruction, draw a figure as fallow: Here, PR = the broken part of the tree $\angle R=30^{0}$ QR = Horizontal line = 8m As per figure, Total height of tree = PQ + PR In $\triangle PQR$ $\cos 30^{0}=\frac {\text {Adjacent side of }\angle R}{Hypotenuse}=\frac {QR}{PR}$ Putting value $\frac {\sqrt {3}}{2}=\frac {8}{PR}$ $PR=\frac {16}{\sqrt {3}}........ (i)$ And also, $\tan 30^{0}=\frac {\text {Opposite side to} \angle R}{\text {Adjacent side of }\angle R}=\frac {PQ}{QR}$ Putting value $\frac {1}{\sqrt {3}}=\frac {PQ}{8}$ $PQ = \frac {8}{\sqrt {3}}........ (ii)$ Hence, total height of tree = PQ+PR $\frac {16}{\sqrt {3}}+\frac {8}{\sqrt {3}}=\frac {16+8}{\sqrt {3}}=\frac {24}{\sqrt {3}}$ multiply by $\sqrt {3}$  $=\frac {24\times \sqrt {3}}{\sqrt {3}\times\sqrt {3}}$ $=\frac {24\times \sqrt {3}}{3}=8\sqrt {3}$

Q3.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

Ans.

Case 1: By construction, In $\triangle ABC$: Height of slide =AB = 1.5 m $\angle ACB = 30^{0}$ We have to find Length of slide AC. We know that: $\sin C = \frac {\text {Opposite side to} \angle C}{Hypotenuse}=\frac {AB}{AC}$ Putting values: $\frac {1}{2}=\frac {1.5}{AC}$ $1\times AC=1.5\times 2$ $AC = 3 \text { m}$ So, Length of slide for below 5 year children = 3 m Case 2: By construction, In $\triangle PQR$: Height of slide = PQ = 3 m $\angle PRQ = 60^{0}$ We have to find Length of slide PR. We know that: $\sin R = \frac {\text {Opposite side to} \angle R}{Hypotenuse}=\frac {PQ}{PR}$ Putting values: $\frac {\sqrt {3}}{2}=\frac {3}{PR}$ $PR = \frac {3\times 2}{\sqrt {3}}=\frac {6}{\sqrt {3}}$ $PR =\frac {6\times \sqrt {3}}{\sqrt {3}\times \sqrt {3}}=\frac {6\sqrt {3}}{3}=2\sqrt{3}$ So, Length of slide for Elder children = $2\sqrt{3}$

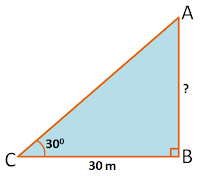
Q4.

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.

Ans.

As per construction; Let Tower is AB Let Point of ground be C Distance of point C from the foot of tower = BC = 30m Angle of elevation = $\angle ACB = 30^{0}$  We have to find height of tower which is AB. In $\triangle ABC$ $\tan C = \frac {\text {Opposite side to }\angle C}{\text {Adjacent side to }\angle C}$ $\tan 30^{0}=\frac {AB}{BC}$ $\frac {1}{\sqrt {3}}=\frac {AB}{30}$ $AB = \frac {30}{\sqrt {3}}$ Multiply by $\sqrt {3}$ $AB = \frac {30\times \sqrt {3}}{\sqrt {3}\times \sqrt {3}}$ $AB = \frac {30\sqrt {3}}{3}=10\sqrt {3}$ Hence, Height of tower (AB) = $10\sqrt {3}$

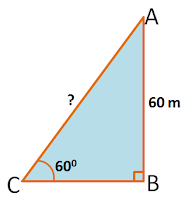
Q5.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

Ans.

As per construction; C is position of kite Kit flying at height = AB = 60 m Inclination of the string with the ground = $\angle ACB = 60^{0}$ We have to find Length of string = Hypotenuse = AC In $\triangle ABC$ $sin C = \frac {\text {Opposite side to }\angle C}{Hypotenuse}=\frac {AB}{AC}$ Putting value $\sin 60^{0}=\frac {60}{AC}$ $\frac {\sqrt {3}}{2}=\frac {60}{AC}$ $AC = \frac {2}{\sqrt {3}}\times 60 = \frac {120}{\sqrt {3}}$ Multiply by $\sqrt {3}$ $AC =\frac {120\times \sqrt {3}}{\sqrt {3}\times \sqrt {3}}$ $AC = \frac {120\sqrt{3}}{3}=40\sqrt {3}\text { m}$ Hence, Length of string $=AC=40\sqrt {3}\text { m}$

Q6.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Ans.

As per given Boy is 1.5 m tall so, PQ = 1.5 m and building is 30 m tall so, AB = 30 m Angle of elevation from start point (Q) to top of building $=30^{0}$ so, $\angle APC = 30^{0}$ When boy moves from point Q to Point R, angle of elevation changes $30^{0}$ to $60^{0}$ So, $\angle ASC = 60^{0}$ and $PQ\parallel CB$, so, we can say that $CQ=CB=1.5\text { m}$ Now, $AC = AB-CB$ $AC = 30-1.5=28.5\text { m}$ And also, $PC\parallel QB$ so, We can say that $PS=QR \text { and } SC = RB$ Since tower is vertical so $\angle ACP = 90^{0}$ Now, In $\triangle APC$ $\tan P = \frac {\text {Opposite side to}\angle P}{\text {Adjacent side to }\angle P}=\frac {AC}{PC}$ Putting value $\tan 30^{0}=\frac {28.5}{PC}$ $\frac {1}{\sqrt {3}}=\frac {28.5}{PC}$ $PC = 28.5\sqrt {3}$ In $\triangle ASC$ $\tan S = \frac {\text {Opposite side to}\angle S}{\text {Adjacent side to }\angle S}=\frac {AC}{SC}$ Putting value $\tan 60^{0}=\frac {AC}{PC}$ $\sqrt {3}=\frac {28.5}{SC}$ $SC = \frac {28.5}{\sqrt {3}}$ Because $PC = PS+SC$ putting value $28.5\sqrt{3}=PS+\frac {28.5}{\sqrt{3}}$ $PS = 28.5\sqrt{3}-\frac {28.5}{\sqrt{3}}$ $PS=\frac {28.5\sqrt{3}\times\sqrt{3}-28.5}{\sqrt{3}}$ $PS=\frac {28.5\times 3-28.5}{\sqrt{3}}$ $PS=\frac {28.5(3-1)}{\sqrt {3}}$ $PS=\frac {28.5\times 2}{\sqrt {3}}$ Multiply by $\sqrt {3}$ $PS=\frac {28.5\times 2}{\sqrt {3}}\times \frac {\sqrt{3}}{\sqrt{3}}$ $PS=\frac {28.5\times \sqrt {3}\times 2}{3}$ $PS=\frac {57\times \sqrt {3}}{3}$ $PS=19\sqrt {3}$ Since $QR=PS$, so, $QR=19\sqrt {3}$ Hence,Walking distance toward the building is $19\sqrt {3}$.

Q7.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

Ans.

As per construction and given; Let Building be AB and Tower be CA Height of building $= AB = 20\text { m}$ Let point on the ground $O$. Angle of elevation from point $O$ to top of building$= \angle AOB = 45^{0}$ Angle of elevation from point $O$ to top of Tower $= \angle COB = 60^{0}$ We have to find $AC$. In $\triangle AOB$, $\tan O = \frac {\text {Opposite side to angle O}}{\text {Adjacent side to angle O}}=\frac {AB}{OB}$ Putting value $\tan 45^{0}=\frac {20}{OB}$ $1=\frac {20}{OB}$ $OB = 20 \text { m}$ and In $\triangle COB$, $\tan O = \frac {\text {Opposite side to angle O}}{\text {Adjacent side to angle O}}=\frac {BC}{OB}$ $\tan 60^{0}=\frac {BC}{OB}$ Putting value $\sqrt {3}=\frac {BC}{20}$ $BC = 20\sqrt {3}$ So, $AB+AC=20\sqrt {3}$ $20+AC=20\sqrt {3}$ $AC=20\sqrt {3}-20$ $AC = 20(\sqrt {3}-1)\text { m}$ Hence, Height of the tower is $20(\sqrt {3}-1)\text { m}$.

Q8.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

Ans.

As per construction and given; Let Pedestal be AB and Statue be CA Height of Statue $= AC = 1.6\text { m}$ Let point on the ground $O$. Angle of elevation from point $O$ to top of Pedestal$= \angle AOB = 45^{0}$ Angle of elevation from point $O$ to top of Statue $= \angle COB = 60^{0}$ We have to find $AB$. In $\triangle AOB$, $\tan O = \frac {\text {Opposite side to angle O}}{\text {Adjacent side to angle O}}=\frac {AB}{OB}$ Putting value $\tan 45^{0}=\frac {AB}{OB}$ $1=\frac {AB}{OB}$ $OB = AB ...................... (i)$ and In $\triangle COB$, $\tan O = \frac {\text {Opposite side to angle O}}{\text {Adjacent side to angle O}}=\frac {BC}{OB}$ $\tan 60^{0}=\frac {BC}{OB}$ Putting value $\sqrt {3}=\frac {BC}{OB}$ $\sqrt {3} OB = BC$ From equation (i) $\sqrt {3} AB = BC$ $\sqrt {3} AB = AB+AC$    $[since BC = AB+AC]$ Putting $AC$ value $\sqrt {3} AB = AB+1.6$  $\sqrt {3} AB -AB = 1.6$  $(\sqrt {3} -1) AB = 1.6$  $AB = \frac {1.6}{\sqrt {3} -1}$ Multiply by $\sqrt {3} +1$ $AB = \frac {1.6}{\sqrt {3} -1}\times \frac {\sqrt {3} +1}{\sqrt {3} +1}$ $AB=\frac {1.6\times (\sqrt {3} +1)}{(\sqrt {3})^{2}-(1)^{2}}$ $AB=\frac {1.6\times (\sqrt {3} +1)}{3-1}$ $AB=\frac {1.6\times (\sqrt {3} +1)}{2}$ $AB = 0.8(\sqrt {3} +1)$ Hence, Height of the Pedestal is $0.8(\sqrt {3} +1)\text { m}$.

Q9.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Ans.

Construct a line diagram as per question. Given: Height of Tower = 50 m = Let = H Height of building, Let = h Distance between tower and building, Let = d Now, In $\triangle ABC$ $\tan 60^{0}=\frac {\text {Opposite side to angle A}}{\text {Adjacent side to angle A}}=\frac {BC}{AB}=\frac {H}{d}$ Putting value $\tan 60^{0}=\frac {H}{d}$ $\sqrt {3}=\frac {50}{d}$ $d=\frac {50}{\sqrt {3}}$ And , In $\triangle ABD$ $\tan 30^{0}=\frac {\text {Opposite side to angle B}}{\text {Adjacent side to angle B}}=\frac {AD}{AB}=\frac {h}{d}$ Putting value $\tan 30^{0}=\frac {h}{d}$ $\frac {1}{\sqrt {3}}=\frac {h}{\frac {50}{\sqrt {3}}}$ $\frac {1}{\sqrt {3}}=\frac {\sqrt {3}h}{50}$ $3h = 50$ $h = \frac {50}{3} = 16.7 \text { m}$

Q10.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

Ans.

$$\begin{align*} \text{Construction :} \quad & \text{Construct a line diagram as per direction given in question} \\ \text{Given:} \quad & \angle APB = 60^\circ, \quad \angle CPD = 30^\circ, \quad AC = 80 \, \text{m} \\ \text{To find:} \quad & \text{The height of the pole} = AB = CD \\ \text{Solution:} \quad & \text{Let } AB \text{ and } CD \text{ be the two poles of equal height, and }\\ & P \text{ be the point on the road between the poles.} \\ & \text{In } \triangle APB,\\ & \tan 60^\circ = \frac{AB}{AP} \\ & \text{or, } AP = AB \cdot \frac{1}{\tan 60^\circ}\\ & \text{or, } AP = \frac {AB} {\sqrt{3}} ........ \quad \text{(i)} \\ & \text{In } \triangle CPD,\\ & \tan 30^\circ = \frac{CD}{CP} \\ & \text{or, } CP = CD \cdot \frac{1}{\tan 30^\circ}\\ & \text{or, } \quad CP = \sqrt{3} CD = \sqrt{3} AB \quad ...........\quad \text{(ii)} \\ & \text{Adding equation (i) and (ii) we get,} \\ & AP + CP = \frac {AB} {\sqrt{3}} + \sqrt{3} AB \\ & \text{or, } AC = AB \left(\sqrt{3} + \frac {1}{\sqrt{3}}\right) \\ & \text{or, } 80 \, \text{m} = 4\cdot \frac {AB} {\sqrt{3}}\\ & \text{or, } \quad AB = 20 \sqrt{3} \, \text{m} \\ & \text{Therefore, height of the pole} = 20 \sqrt{3} \, \text{m} \approx 34.64 \, \text{m} \end{align*}$$

Q11.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.

Ans.

$$\begin{align*} \text{Given that: } & AB \text{ Height of tower and }\\ & AC \text{ width of canal.}\\ & C \text{ is the point on the other side} \\ & \text {of the canal directly opposite the tower.} \\ & \text{Let } AB = h, \quad CA = x, \quad CD = 20 \\ \text{Solution: } & \text{In } \triangle BAC:\\ & \cot 60^\circ = \frac{x}{h} \\ & \text{or, } \frac{1}{\sqrt{3}} = \frac{x}{h}\\ & \text{or, } x = \frac{h}{\sqrt{3}} ........... \text{(i)} \\ & \text{In } \triangle BAD:\\ & \cot 30^\circ = \frac{AD}{AB} \\ & \text{or, } \sqrt{3} = \frac{x+20}{h} \\ & \text{or, } x = h\sqrt{3} - 20 ........... \text{(2)} \\ & h = 10\sqrt{3} \\ & \text{From equation } (1):\\ & x = \frac{10\sqrt{3}}{\sqrt{3}} = 10 \\ & \text{Therefore, the width of the canal = } 10\text{m}.\\ & \text{and the height of the canal = } 10\sqrt{3} \, \text{m}. \end{align*}$$

Q12.

From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.

Ans.

$$\begin{align*} \text {Construction: }& \text {Construct a line diagram as per question}\\ & \text{Let, the height of the tower = } CE\\ & \text{ the height of the building = } AB\\ & \text{The angle of elevation } \angle EAD = 60^\circ \\ & \text{the angle of depression} \angle ACB = 45^\circ \\ & \text{Draw } AD \parallel BC\\ & \text{Then, } \angle DAC = \angle ACB = 45^\circ \text{ (alternate interior angles)} \\ \text {Solution :} & \text{In } \triangle ABC:\\ & \tan 45^\circ = \frac{AB}{BC}\\ & \text{or, } 1 = \frac{7}{BC} \\ & \text{or, } \quad BC = 7 \\ & ABCD \text{ is a square, so: } BC = AD = 7 \quad \text{and} \quad AB = CD = 7 \\ & \text{In } \triangle ADE:\\ & \tan 60^\circ = \frac{ED}{AD} \\ & \text{or, } \sqrt{3} = \frac{ED}{7}\\ & \text{or, } ED = 7\sqrt{3} \\ & \text{As per construction, Height of the tower } CE = ED + CD\\ & CE = 7\sqrt{3} + 7 = 7(\sqrt{3} + 1) \\ & \text{Therefore, height of the tower }= 7 (\sqrt{3} + 1) \, \text{m.} \end{align*}$$

Q13.

As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.

Ans.

$$\begin{align*} \text {Given :} & \text { Height of Lighthouse = } 75 \text {m}\\ & \text {Let, Two ships be at point C and D, so }\\ & \text {Angle of depression with ship D =} 30^\circ \\ & \text {Angle of depression with ship C =} 45^\circ \\ \text {Construction :} & \text {Construct line diagram as per question, Where}\\ & AB = \text {Lighthouse height =} 75 \text {m}\\ \text {Solution :} & \text {In} \triangle ABC,\\ & \Rightarrow \tan 45^\circ = \frac {AB}{BC}\\ & \Rightarrow 1=\frac {75}{BC}\\ & \Rightarrow BC = 75 \text { m}\\ & \text {In} \triangle ABD,\\ & \Rightarrow \tan 30^\circ = \frac {AB}{BD}\\ & \text {As per construction BD = BC + CD, So}\\ & \Rightarrow \frac {1}{\sqrt {3}}=\frac {75}{BC + CD}\\ & \Rightarrow \frac {1}{\sqrt {3}}=\frac {75}{75 + CD}\\ & \Rightarrow 75\sqrt {3} = 75 + CD\\ & \Rightarrow CD = 75\sqrt {3} - 75\\ & \Rightarrow CD = 75 (\sqrt {3} - 1)\\ & \text {By taking } \sqrt {3} = 1.73, We get \\ & CD = 54.75 \text { m}\\ & \text {Hence, the distance between two ship = 54.75 m}. \end{align*}$$

Q14.

A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.

Ans.

$$\begin{align*} \text{Given:} \quad & \text{Height of girl = AG = 1.2 m} \\ & \text{Also, } AG \parallel BF \\ & \text {So,}BF = AG = 1.2 \, \text{m}\\ & \text{height of Baloon}= EF = 88.2 \, \text{m} \\ & \text{Girl sees the balloon first at } 60^\circ \\ & \text{After change, the angle of elevation becomes } 30^\circ \\ & \text{So, Distance traveled by the balloon} = BC \\ & \text{Now, } BE = EF - BF = 88.2 - 1.2 = 87\, \text{m} \\ & \text{Also, } BE = DC = 87 \, \text{m} \\ & \text{Here, } \angle ABE = 90^\circ \text{ and } \angle ACD = 90^\circ \\ \text {Solution :} & \text{In } \triangle EBA\\ & \tan A = \frac{BE}{AB}\\ & \text {Putting value}\\ & \text{or, }\tan 60^\circ = \frac{87}{AB} \\ & \Rightarrow \sqrt{3} = \frac{87}{AB}\\ & \Rightarrow AB = \frac {87}{\sqrt{3}} \, \text{m} \\ & \text{In } \triangle DAC:\\ & \tan A = \frac{CD}{AC} \\ & \text{or, } \tan 30^\circ = \frac{87}{AC} \\ & \Rightarrow \frac{1}{\sqrt{3}} = \frac{87}{AC}\\ & \Rightarrow AC = 87\sqrt{3} \, \text{m} \\ & \text{Now, as per construction } AC = AB + BC \\ & \text {Putting value}\\ & \Rightarrow 87\sqrt{3} = \frac {87}{\sqrt{3}} + BC \\ & \Rightarrow BC = 87\sqrt{3} - \frac {87}{\sqrt{3}} \\ & \Rightarrow BC = 87\left(\sqrt{3} - \frac {1}{\sqrt{3}}\right) \\ & \Rightarrow BC = 87\left(\frac {3-1}{\sqrt {3}}\right) \\ & \Rightarrow BC = 87\times \frac {2}{\sqrt {3}} \\ & \text {Multiply by } \sqrt {3}\\ & \Rightarrow BC = 87\times \frac {2}{\sqrt {3}}\times \frac {\sqrt {3}}{\sqrt {3}} \\ & \Rightarrow BC = 87\times \frac {2\sqrt {3}}{3} \\ & \Rightarrow BC = 29\times 2\sqrt{3} \\ & \Rightarrow BC = 58\sqrt{3} \\ & \text{Hence, the distance traveled by the balloon} = 58\sqrt{3} \, \text{m} \end{align*}$$

Q15.

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.

Ans.

$$\begin{align*} \text {Construction :} & \text{Let, the tower be } AB \\ & \text{Initial position of Car = D} \\ & \text { Final position of the car = C} \\ & \text{Angles of depression are measured from A.}\\ & \text {Distance between the foot of the tower to the car = BC} \\ \text {Solution :} & \text{In } \triangle ABC:\\ & \tan 60^\circ = \frac{AB}{BC}\\ & \text{or, } \sqrt{3} = \frac{AB}{BC}\\ & \text{or, } BC = \frac{AB}{\sqrt{3}}....... (i) \\ & \text{Also, In } \triangle ABD:\\ & \tan 30^\circ = \frac{AB}{BD}\\ & \text{or, } \quad \frac{1}{\sqrt{3}} = \frac{AB}{BC + CD} \\ & \text{or, } \quad AB\sqrt{3} = BC + CD \\ & \text{or, } \quad CD = AB\sqrt{3}-BC\\ & \text {Putting BC value from equation (i)}\\ & \text{or, } \quad CD = AB\sqrt{3}-\frac {AB}{\sqrt{3}} \\ & \text{or, } \quad CD = AB(\sqrt{3} - \frac{1}{\sqrt{3}}) \\ & \text{or, } \quad CD = \frac {2AB}{\sqrt{3}}\\ & \text{or, } \quad AB = \frac{\sqrt{3}CD}{2} ...... (ii)\\ & \text{Substitute this } AB \text{ value frome equ. (ii) to equ. (i) } :\\ & BC = \frac{\sqrt{3}CD}{2\sqrt{3}} \quad \text{or, } \quad BC = \frac{CD}{2} \\ & \text{Here, the distance of } BC \text{ is half of } CD.\\ & \text{Thus, the time taken is also half.} \\ & \text{Time taken by car to travel distance } CD \text{ is 6 seconds.} \\ & \text{Time taken by car to travel BC is } \frac{6}{2} = 3 \, \text{seconds} \end{align*}$$